Στην εξαναγκασμένη ταλάντωση ενός συστήματος ελατηρίου-μάζας ασκούνται οι δυνάμεις:
η
ελαστική δύναμη -kx,
με k=mωο2, η δύναμη απόσβεσης
και η δύναμη από το διεγέρτη, τη συνισταμένη των οποίων ονομάζω έστω F’.
Έτσι από
το 2ο νόμο του Newton για την
κίνηση έχουμε
–kx + F’= mα και επειδή α=–ωδ2x
–kx + F’= – mωδ2x.
F’= -m(ωδ2-ω02)x
Τότε:
Αν ωδ>ωο τότε F’=–m(ωδ2–ωο2)×x,
οπότε:
όταν x>0
τότε F’<0 ενώ όταν x<0 τότε F’>0
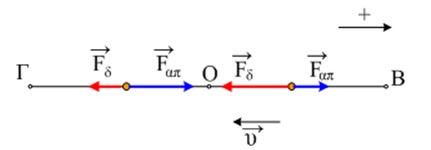
Έστω λοιπόν ότι το σώμα ξεκινά
από την ακραία θέση Β, στην οποία έχει μια ορισμένη τιμή δυναμικής ενέργειας Umax και
κινείται προς τα αριστερά. Στο σχήμα εμφανίζονται οι δυνάμεις που ασκούνται στο
σώμα.
Το έργο της συνισταμένης (των Fδ και
Fαπ) F’ είναι θετικό στην κίνηση προς τη Θ.Ι. Ο και
αρνητικό προς την ακραία θέση Γ, οπότε η μέγιστη κινητική ενέργεια θα είναι μεγαλύτερη
από τη μέγιστη δυναμική ενέργεια κατά το έργο τη F΄.
Δείτε όλη την απόδειξη από εδώ.

Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου